Merge Sort Algorithm – Explanation, Implementation and Complexity

Merge Sort is a divide and conquers algorithm in which original data is divided into a smaller set of data to sort the array.

In merge sort the array is firstly divided into two halves, and then further sub-arrays are recursively divided into two halves till we get N sub-arrays, each containing 1 element.
Then, the sub-arrays are repeatedly merged, to produce new array until there is one array remaining. This will be our sorted array at the end.

Here are some key points of merge sort algorithm –

• Merge Sort is a type of recursive algorithm.
• We can express time complexity of merge sort by this recurrence relation: T(n) = 2T(n/2) + O(n)
  Using Masters Theorem, we get -> T(n)=O(n*logn).
• Time complexity of Merge Sort is O(n*logn) in all 3 cases (worst, average and best) as in merge sort , array is recursively divided into two halves and take linear time to merge two halves.
• It is not an in-place sorting algorithm as it requires additional scratch space proportional to the size of the input array.
• It requires an equal amount of additional space as the unsorted list. Hence, it’s not at all recommended for sorting large size list.
• Merge Sort is a stable sort, which means the “equal” elements appear in the same order in the sorted array as they were in the unsorted array.
• Merge Sort is a best-sorting technique for sorting Linked Lists. Because in linked list it can be implemented without extra space as elements can be inserted in the middle in O(1) extra space and O(1) time.

Let’s understand it with an example of odd size array–

Observe each step in the image below carefully and try to visualize the concept of this algorithm.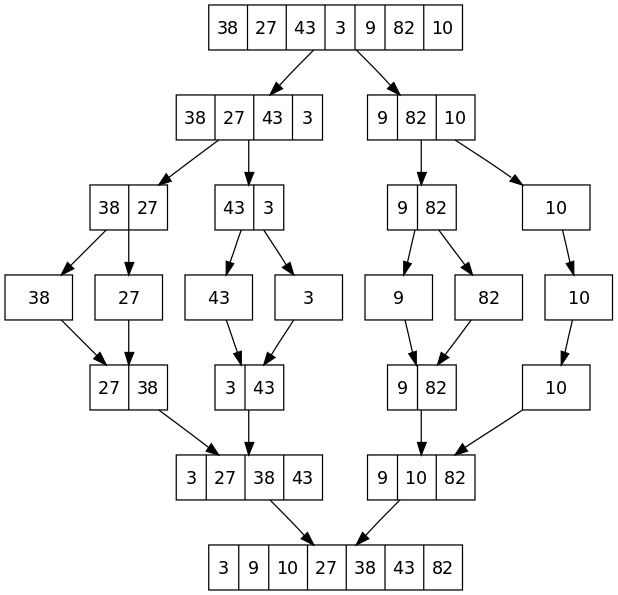

So in the above picture we see that the size of the array is (n=7). As we know |7/2|=3, so while the first division of array, the size of one part will be 3 and another part will be (7-3=4).

Similarly, the array will recursively divide into two halves till we get all sub-array containing of exactly 1 element. Then each element is compared with the adjacent array to sort and merge the two adjacent arrays till the complete array is merged. Finally, all the elements are sorted and merged.

Pseudocode of Merge Sort

//A->array, l->left most index, r->right most index
MERGE-SORT(A, l, r)
    if  l < r
        mid = (l+(r-l)/2)
    MERGE-SORT(A, l, mid)
    MERGE-SORT (A, mid+1, r)
    MERGE(A, l, mid ,r)
end func

MERGE(A, l, m, r)
    nL = m-l+1
	nR = r-m
    Create arrays L[1..nL+1] and R[1..nR+1]
	for  i=0 to nL-1
		L[i] = A[l+i]
	end for
	for j=0 to nR-1
		R[j] = A[m+l+j]
    end for

	i=0;  j=0;  k=l;
	while  i < nL and j < nR
        if  L[i] <= R[j]
            A[k]=L[i];  i=i+1;  k=k+1;
		else
            A[k]=R[j];  j=j+1;  k=k+1;
	end while

	while  i < nL
        A[k]=L[i];  i=i+1;  k=k+1;
	end while

	while  j < nR
		A[k]=R[j];  j=j+1;  k=k+1;
	end while
end func

Asymptotic Analysis of Merge Sort

Since in this algorithm array is recursively divided into two halves and take linear time to merge two halves, so the complexity of this algorithm id O(n*logn) in all the cases. Summarizing all this-

Worst Case Time complexity: O (n*logn)
Average Case Time complexity: O(n*logn)
Best Case Time complexity: O(n*logn)
Space Complexity: O(n) Auxiliary space
Algorithmic Paradigm: Divide and Conquer
Sorting In Place: No
Space Complexity: O(n)
Stable: Yes

Implementation of Merge Sort in C programming language

//C program for Merge Sort
#include<stdlib.h>
#include<stdio.h>

// Merges two sub-arrays A[l..m] and A[m+1..r].
// l->left most index, r->right most index, m->middle index
void merge(int A[], int l, int m, int r)
{
    int i, j, k;
    //Find sizes of two sub-arrays to be merged
    int nL = m - l + 1;
    int nR =  r - m;

    /* create temp Arrays left[] and right[]
    and copy data from main array */
    int left[nL], right[nR];
    for (i = 0; i < nL; i++)
        left[i] = A[l + i];
    for (j = 0; j < nR; j++)
        right[j] = A[m + 1+ j];

    /* Merge the temp Arrays back into A[l..r]*/
    i = 0; // Initial index of first subArray
    j = 0; // Initial index of second subArray
    k = l; // Initial index of merged subArray

    /* Comparing left[] and rigth[], sub-array with
        smaller element get copy to main array A[]*/
    while (i < nL && j < nR)
    {
        if (left[i] <= right[j])
        {
            A[k] = left[i];
            i++;
        }
        else
        {
            A[k] = right[j];
            j++;
        }
        k++;
    }

    /* Copy the remaining elements of left[], if there
       are any */
    while (i < nL)
    {
        A[k] = left[i];
        i++;
        k++;
    }

    /* Copy the remaining elements of right[], if there
       are any */
    while (j < nR)
    {
        A[k] = right[j];
        j++;
        k++;
    }
}

/* l is for left index and r is right index of the
   sub-Array of A to be sorted */
void merge_sort(int A[], int l, int r)
{
    if (l < r)
    {
        // Same as (l+r)/2, but avoids overflow for large l
        int mid = l+(r-l)/2; //mid is middle index

        // Sort first and second halves
        merge_sort(A, l, mid); //Firstly left half is recursively call
        merge_sort(A, mid+1, r);// Then right half is recursively call

        merge(A, l, mid, r); //merge function call
    }
}

/* UTILITY FUNCTIONS */
/* Function to print an Array */
void printArr(int A[], int size)
{
    int i;
    for (i=0; i < size; i++)
        printf("%d ", A[i]);
        printf("
");
}

/* Program to test above functions */
int main()
{
    int A[] = {38, 27, 43, 3, 9, 82, 10};
    int arr_size = sizeof(A)/sizeof(A[0]);

    printf("Unsorted Array: 
");
    printArr(A, arr_size); // Print unsorted array

    merge_sort(A, 0, arr_size - 1);

    printf("
Sorted Array: 
");
    printArr(A, arr_size);// Print sorted array
    return 0;
}

Output:-
Unsorted array: 38 27 43 3 9 82 10
Sorted array:  3 9 10 27 38 43 82

Implementation of Merge Sort in Java programming language

package com.codingeek;
import java.util.*;
/* Java program for Merge Sort */
public class MergeSort
{
    // Merges two sub-Arrays A[l..m] and A[m+1..r].
	 // l->left most index, r->right most index, m->middle index
    void merge(int A[], int l, int m, int r)
    {
        // Find sizes of two subArrays to be merged
        int nL = m - l + 1; //for left sub-array
        int nR = r - m; //for right sub-array
 
        /* create temp Arrays left[] and right[]
        and copy data from main Array */
        int left[] = new int [nL];
        int right[] = new int [nR];
 
        for (int i=0; i<nL; ++i)
            left[i] = A[l + i];
        for (int j=0; j<nR; ++j)
            right[j] = A[m + 1+ j];
 
        /* Merge the temp Arrays back into A[l..r]*/
        
        // Initial indexes of first and second sub-Arrays
        int i = 0,j = 0;
        int k = l;  // Initial index of merged sub-array
        
        /* Comparing left[] and right[], sub-Array with
        smaller element get copy to main Array A[]*/
        while (i < nL && j < nR)
        {
            if (left[i] <= right[j])
            {
                A[k] = left[i];
                i++;
            }
            else
            {
                A[k] = right[j];
                j++;
            }
            k++;
        }
        /* Copy remaining elements of left[] if any */
        while (i < nL)
        {
            A[k] = left[i];
            i++;
            k++;
        }
        /* Copy remaining elements of right[] if any */
        while (j < nR)
        {
            A[k] = right[j];
            j++;
            k++;
        }
    }
 
    // Main function that sorts A[l..r] using merge()
    /* l is for left index and r is right index of the
    sub-Array of A to be sorted */
    void merge_sort(int A[], int l, int r)
    {
        if (l < r)
        {
            int mid = (l+r)/2; // Find the middle index

            merge_sort(A, l, mid); //Firstly left half is recursively call
            merge_sort(A , mid+1, r); // Then right half is recursively call
            merge(A, l, mid, r); // Merge the sorted halves
        }
    }
    // Driver method
    public static void main(String args[])
    {
        int Arr[] = {38, 27, 43, 3, 9, 82, 10};
        
        System.out.println("Unsorted Array:");
        //print unsorted array using Arrays.toString()
        System.out.println(Arrays.toString(Arr));
       
        //object of class MergeSort
        MergeSort ob = new MergeSort();
        ob.merge_sort(Arr, 0, Arr.length-1);//merge sort function call
 
        System.out.println("
Sorted Array:");
        System.out.println(Arrays.toString(Arr)); //print sorted array
    }
}

Output:-
Unsorted array: 38 27 43 3 9 82 10
Sorted array:  3 9 10 27 38 43 82

That’s all for merge sort, one of the most respected and important sorting algorithms. As a coder, you should be aware of this algorithm and it is quite fast with time complexity of O(n log n). Always use merge sort or quick sort for faster and efficient programming. In java use Collections.sort() method as it also uses merge sort internally( but now in newer java versions TimSort is being used).

Knowledge is most useful when liberated and shared. Share this to motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.

Keep Learning… Happy Learning.. 🙂

Recommended -