Binary Heap – Introduction, Explanation and Implementation

A heap is a tree based data structure that follows,

• It’s a complete tree , all the levels are completely filled except possibly the last level where all keys(nodes) are as left as possible.
• A heap is always defined as a Min heap and Max Heap. If the key is always greater than their children, then, Max heap. In case smaller, than Min heap.

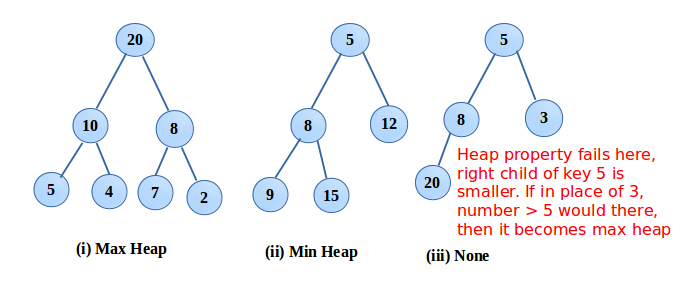
Among all heaps, binary heap is more widely used. Here onwards, we’ll be covering binary heap. Since heap is a complete tree. Therefore, binary heap is a complete binary tree.

Whenever we need to find the maximum value among the given set of items and it is needed to be fetched out frequently then binary heap is used.

Why couldn’t use other data structure:

• Linked list, searching of max key causes alone O(n).
• Ordered array, searching of max key causes O(1) but then extracting it causes O(n) to reorder it.
• Heap, Searching of max key takes O(1) and reordering takes O(logn). Interstingly, insertion is also taking not more than O(logn). Thus, heap is most suited.
  Moreover, heap is implemented using array. Hence it’s not memory consuming like linked list.

Operations in Heap:

These are the operations performed in a heap.

1. Insertion – Refers to inserting of keys.

   

2. GetMax/getMin –  Finding out the max key/min key.
3. ExtractMax/ExtractMin – This is frequently used, extracting the max key. Similarly, the other one ExtractMin means extracting the min key.

   

4. IncreaseKey/decreaseKey – This refers to the increasing the key at a desired index.

   

Implementation:

Heap is implemented using array. Following is the implementation of heap in C, where structure is defined. The structure contains Heap, its max capacity, the size of heap.

#include<stdio.h>
#include<stdlib.h>

typedef struct HeapDataStructure{
	unsigned short heapSize;
	unsigned short capacity;
	int *heap;
}Heap;
	
Heap *createHeap(unsigned short );
Heap *increaseKey(Heap *, int , int );
Heap *maxHeapify(Heap *, int );
Heap *insert(Heap *, int );
Heap *extractMax(Heap *);
int getMax(Heap *);
void swap(int *, int *);
void printHeap(Heap *);
	
/* on calling it, creates a heap data structure*/	
Heap *createHeap(unsigned short capacity){	
	Heap *maxHeap;
	maxHeap = (Heap *)malloc(sizeof(Heap));
	maxHeap->heap = (int *)malloc( sizeof(int)*capacity );
	maxHeap->capacity = capacity;
	maxHeap->heapSize = 0;
	
	return maxHeap;
}
			
void swap(int *p, int *q){
	int temp;
	temp = *p;
	*p = *q;
	*q = temp;
}
	
/* inserting key to maxHeap, this would take O(logn)*/	
Heap * insert(Heap *maxHeap, int key){
	int temp = maxHeap->heapSize;
	
	if(maxHeap->heapSize == maxHeap->capacity)
		printf("\nHeap overflow");
		
	maxHeap->heapSize++ ; //size of heap increamented by 1
	maxHeap->heap[temp] = key; //storing key to heap, stored at the last index of array	
	
	if(maxHeap->heapSize == 1)
		return maxHeap;
		
	/* 1) n case heapSize > 1, new key is supposed to follow maxKey property,
	 * thus, comparing with its parent and to grand parents.
	 * 2) (temp-1)/2, index of the parent of a key
	 * 3) This while loop takes O(logn) time*/	
	while(maxHeap->heap[(temp-1)/2] < key && temp != 0){
		maxHeap->heap[temp] = maxHeap->heap[(temp-1)/2];
		temp = (temp-1)/2;
	}
	maxHeap->heap[temp] = key;
	
	return maxHeap;
}
/*increasing the a key at given index */
Heap *increaseKey(Heap *maxHeap, int nKey, int index){
	int temp;
	
	if(maxHeap->heap[index] >= nKey)
		printf("\nInvalid operation");
	else{
		maxHeap->heap[index] = nKey;
		temp = index;
		while(maxHeap->heap[(temp-1)/2] < nKey && temp != 0){
			maxHeap->heap[temp] = maxHeap->heap[(temp-1)/2];
			temp = (temp-1)/2;
		}
		maxHeap->heap[temp] = nKey;
	}
		
	return maxHeap;	
}	
	
Heap *maxHeapify(Heap *maxHeap, int i){
	
	int L, R, largest; // L as left, R as right
	
 /*children key at i are at 2*i+1 and 2*i+2, as index starts with 0*/	
	L = 2*i+1;
	R = 2*i+2; 
	
	if(L <= maxHeap->heapSize-1 && maxHeap->heap[L] > maxHeap->heap[i])
		largest = L;
	else 
		largest = i;
	
	if(R <= maxHeap->heapSize-1 && maxHeap->heap[R] > maxHeap->heap[largest])
		largest = R;
	
	if(largest != i){
		swap(&(maxHeap->heap[i]), &(maxHeap->heap[largest]));
		maxHeapify(maxHeap, largest);
	}
	return maxHeap;
}		
/*it extracts the maxkey of the heap, which will be at root(index 0) */
Heap *extractMax(Heap *maxHeap){
	int temp, extractedKey;
	
	if(maxHeap->heapSize == 0){
		printf("\nHeap Underflow");
		return maxHeap;
	}
	else{
		temp = maxHeap->heapSize-1;
		//swaping lastKey to root and decreasing the heapSize by 1
		extractedKey = maxHeap->heap[0];
		maxHeap->heap[0] = maxHeap->heap[temp];
		maxHeap->heapSize--;
		
		maxHeap = maxHeapify(maxHeap, 0); 	
		
		printf("\nKey Extracted:%d", extractedKey);
		return maxHeap;
	}
}
	
int getMax(Heap *maxHeap){
	return maxHeap->heap[0];
}

void printHeap(Heap *maxHeap){
	int i;
	printf("\nKeys in Heap:");
	for( i = 0; i < maxHeap->heapSize; i++ )
		printf("%d ", maxHeap->heap[i]);
}

int main(void){
	
	int getMaxKey;
	
	Heap *maxHeap;
	unsigned short capacity  = 10; //max size of heap is 10
	maxHeap = createHeap(capacity);
	
	/* creating a heap with 5, 10, 40, 30, 20*/
	maxHeap = insert(maxHeap, 5);
	maxHeap = insert(maxHeap, 10);
	maxHeap = insert(maxHeap, 40);
	maxHeap = insert(maxHeap, 30);
	maxHeap = insert(maxHeap, 20);
		
	printHeap(maxHeap);
	
	getMaxKey = getMax(maxHeap);
	printf("\nMaxKey: %d\n",getMaxKey);
	
	maxHeap = increaseKey(maxHeap, 7, 2); //increaseKey(Heap* ,nKey, index )	
	printHeap(maxHeap);
		
	maxHeap = increaseKey(maxHeap, 50, 1);
	printHeap(maxHeap);	
	
	maxHeap = extractMax(maxHeap);
	printHeap(maxHeap);
		
	return 0;
}

Output:-

Keys in Heap:40 30 10 5 
MaxKey: 40
Invalid operation
Keys in Heap:40 30 10 5 
Key Extracted:40
Keys in Heap:30 5 10 

Applications:-

1. Using heap, sorting can be done and it is named as Heapsort. Interestingly, heapsort takes O(nlogn).
2. Priority Queue is implemented using heap.
3. Dijkstra’s shortest path algorithm uses heap.
4. Prim’s minimum spanning tree algorithm reduces the run time by polynomial order.
5. Finding kth smallest/greatest key.

Knowledge is most useful when liberated and shared. Share this to motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.
Keep Learning… Happy Learning.. 🙂

Recommended -