Priority Queue – Introduction, Explanation and Implementation

Priority Queue is a data structure which is similar to Queue and Stack. Moreover, it is an extension to queue with following properties

• Each item is associated with a priority
• Items are served(Insert/Delete) keeping priority into consideration
• Items with same priority are served as per their order in queue

A priority queue supports the following operations:

• Insertion(enqueue) – refers to insertion of item along with its associated priority
• Deletion(dequeue) – refers to deletion of item with highest priority
• Peek – refers to getting an item with the highest priority. This one is frequently used.

Interestingly, it’s worth noting Stack and Queue can be seen as a particular kind of Priority Queue.
See

In the above picture, priority of item is increasing up to the top i.e. newly inserted item will always have the highest priority and thus, deleted back first. Therefore, a stack can be said as a Priority Queue where priority of items is kept on increasing monotonically.

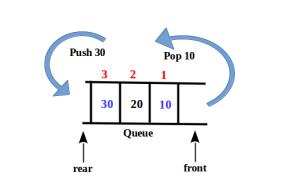
In the above picture, priority of item is increasing towards rear side and decreasing towards front side. As deletion is always subject to removing higher priority item, therefore, Queue can also be said as a Priority Queue in which priority of items is kept on decreasing monotonically.

Implementation:

There can be a number of approaches to implement priority queue however, Heap is preferred(look at the table). Other implementations are just for the sake of understanding and visualizing. Like, it can be implemented using an unordered array, where deletion operation requires fetching the highest priority key/item and remove it accordingly.

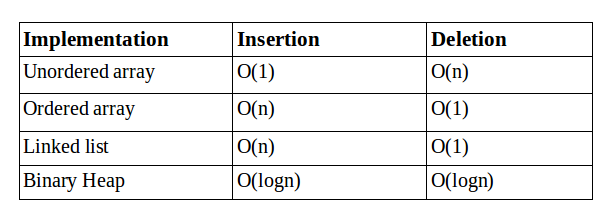
We can also apply sorting algorithm but then it’ll take O(n*logn) which is worst. Hence, heap is preferred. Fibonacci heap can also be used.

Implementation in C:

The following priority queue, implemented using linked list where each item is associated with some priority and no two elements can have same priority but there could be multiple implementations for ex, an implementation in which we can have multiple elements with the same priority and sort them based on their value.

#include<stdio.h>
#include<stdlib.h>
 
typedef struct priorityQueueNode{
    int item;
    int priority;
    struct priorityQueueNode *next;
    }pqNode;
 
/*It takes O(n) time to search for same priority and O(1) to insert the item*/
pqNode * push(pqNode *head, int item, int priority){
 
    pqNode *list = head;
    pqNode *temp = (pqNode *)malloc(sizeof(pqNode));
 
    while(list){
        if(list->priority == priority){
            printf("An item with the same priority already exists\n");
                return head;
        }
    list = list->next;
    }/*checking if the new item possess existing priority  */
 
    temp->item = item;
    temp->next = NULL;
    temp->priority = priority;
     
    list = head;
    printf("Item %d pushed\n", item);
    if(list == NULL)
        return temp;
    else{
        temp->next = list;
        return temp;
        }
}
 
/* It takes O(n) time to search the highest priority item and O(1) to delete */
pqNode * pop(pqNode *head){
 
    pqNode *list = head;
    pqNode *temp = NULL;
    pqNode *p = NULL, *q = NULL;
 
    int maxPriority = 0; //to find the item with highest priority
 
    if(!list){
        printf("\nUnderflow");
        return list;
    }
    else if(!list->next)
        return NULL;
    else{
        while(list){            
            if(list->priority > maxPriority){
                maxPriority = list->priority;
                p = temp;  //pointing to previous to the highest priority node
                q = list;  //pointing the highest priority node
            }
            temp = list;
            list = list->next;
        }
        p->next = q->next;
        printf("Item %d deleted\n", q->item);
        free(q);
        return head;
    }   
}
 
void peek (pqNode *head){
 
    pqNode *list = head;
    int maxPriorityItem;
    int maxPriority = 0;
 
    if(!list)
        printf("List is empty\n");
         
    while(list){
        if(list->priority > maxPriority){
            maxPriority = list->priority;
            maxPriorityItem = list->item;
        }       
        list = list->next;
    }
    printf("Highest priority item: %d\n", maxPriorityItem);
}   
 
int main(void){
 
    pqNode* head;
    pqNode* first = (pqNode*)malloc(sizeof(pqNode)); 
    pqNode* second = (pqNode*)malloc(sizeof(pqNode));
     
    //ASSIGNINMENT
    first->item = 2000; //assign data in first node along with the priority
    first->priority = 5;
    first->next = second; // Link first node with second 
 
    second->item = 1000; //assign data to second node along with the priority
    second->priority = 8;
    second->next = NULL;
 
    head = first;    //head pointing to the list
 
    head = push(head, 5000, 6);
    peek(head);
    head = pop(head);
    peek(head);
    head = push(head, 3000, 5); //operation will be dropped as priority 5 already exists
    return 0;
}

Output:-

Item 5000 pushed
Highest priority item: 1000
Item 1000 deleted
Highest priority item: 5000
An item with the same priority already exists

Applications:

• The Popular algorithm, Dijkstra’s Shortest path algo and Prim’s minimum spanning tree are priority queue based.
• Scheduling algorithm in operating system.
• Huffman coding algorithm used in data compression.

Knowledge is most useful when liberated and shared. Share this to motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.
Keep Learning… Happy Learning.. 🙂

Recommended -